Fast calculation of sin and cos

By Paul Dreik 2020-08-31

I was profiling a very niche C++ application for a client and found out that it spend a significant amount of time calculating sin and cos. Inspecting the code, I could see that the application did not need full accuracy and could perhaps benefit from having a faster, but approximate, implementation.

This lead me down to a long and interesting route of looking at how sin is calculated. I decided to write down some notes along the way.

I had a lot of thoughts:

• how is sin actually calculated? Hardware support, series expansion, table lookup?
• is there anything to turn off, like exceptions, corner case checking that I do not need for my application?
• how much is there to gain, is it worth it?

How is std::sin(double) implemented on GNU?

I work in Debian, which uses the GNU standard library. Behold the beauty of open source! I installed the source code with apt source libc6-dev so I could browse it locally. There were multiple implementations and source files related to this, so I decided to use the debugger to point me to the exact source that was being used. I wrote a toy program invoking sin and ran it in the debugger. It uses bogus input and writes the result, so the compiler does not optimize it away.

#include <math.h>
int main(int argc,char* argv[]) {
  double x=sin(argc*1.0);
  return x;
}

I then compiled it with

gcc -g -lm prog.c -o prog

and ran it in gdb (having apt installed the libc6-dbg package first)

gdb prog
(gdb) run x
Starting program: /tmp/prog x

Breakpoint 1, sin_ifunc_selector () at ../sysdeps/x86_64/fpu/multiarch/ifunc-avx-fma4.h:32
32  ../sysdeps/x86_64/fpu/multiarch/ifunc-avx-fma4.h: Filen eller katalogen finns inte.
(gdb) step
__sin_fma (x=2) at ../sysdeps/ieee754/dbl-64/s_sin.c:205
205 ../sysdeps/ieee754/dbl-64/s_sin.c: No such file or directory

Installing the source is as easy as

apt source glibc

and to see it in gdb, run the following before starting the program:

directory glibc-2.28/sysdeps/

This is great, because now I am certain which code actually implements sin() on my system. The code can be browsed here in the upstream repo on sourceware.

The implementation seems to be written by IBM and there is a lot of magic going on, reading doubles through unions, magic constants and a lot of tricks. It is not easy to get full accuracy throughout the entire range of input values.

Interestingly, the double and float versions seem to be quite different.

The overall strategy is, simplified:

• if the input is tiny (less than approximately 2^-52/3), use the approximation sin(x)=x since the approximation error is smaller than what can be preserved in the 52 bit mantissa. Also, this case has to handle underflow correctly.
• if the input is small (<0.85), use a Taylor expansion. Also, a correction is made by looking up polynomial coefficients from a pretty big table.
• if the input is slightly larger, use the identity sin(x)=cos(pi/2-x) and use Taylor and a correction table for cos
• if the input is large, use a range reduction and proceed with the previous strategy.

The source includes tables of precomputed values, and no special hardware support like SIMD or special instructions are used, even if the compiler obviously is free to optimize it into using those.

This made me think - the performance of std::sin() is data dependent:

• the data tables may be or not in cache
• if one has for instance very small values such as 0, the execution takes the fast path above instead of the more involved calculations
• the branch predictor may learn what is happening, and speed up the access pattern of your program if it can. Say for instance calculating sin for an increasing value, the same path is probably taken through the program each time.

Below, I try to go through the steps.

Approximating sin() with polynomials

All implementations and mentions of how to calculate sin used variations of Taylor expansion as part of the calculation.

See the Wikipedia article on Taylor series which uses sin() as an example with nice illustrations.

The GNU implementation uses a different order at different places. When a correction is used from table lookup, a fifth order (x^5) polynomial is used for the initial approximation, followed by higher order correction polynomial. For small arguments which do not use the table for correction, the highest term is x^11.

Range reduction

Mathematically, sin(x+n2pi)=sin(x) with an integer n. To be able to use the series expansion, one needs to remove the excess rotation. This is tricky, because it may lose precision.

Reading about this lead me to the ARGUMENT REDUCTION FOR HUGE ARGUMENTS: Good to the Last Bit article from 1992, by K. C. Ng.

There is also an interesting answer on stack overflow discussing how accuracy is increased by something called Cody-Waite argument reduction.

The range reduction in GNU sin is a bit difficult to comprehend. Besides preserving accuracy, it also returns which quadrant the argument lies in so the implementation can use symmetry for sin/cos to reuse the implementation all around the circle.

Error handling

NaN, +-Inf and excessive input have to be handled. On top of this, errno has to be set.

Benchmarking GNU std::sin(double)

I wrote a program (find the source on github) with three sets of input data. Note, the numbers below are not very accurate because they were found using a laptop and short running time. Also, I sum the numbers up to prevent the compiler from removing the benchmark code so the numbers below over estimate the time consumption.

• Tiny, where numbers with very small absolute amplitude are used (less than 1e-30)
• linear, where angels increase from 0 to 100pi over 3000 samples
• garbage, which is bitwise random data. Because of how floats are represented, this mostly gives input with huge input, 1e300 or so.

With AVX enabled using gcc 8 on a skylake laptop with cpu i7-8565U I got (when compiled with -O3 -mavx2 -mfma)

• Tiny: 2.86616e+08 values per second.
• Linear: 1.03997e+08 values per second.
• Garbage: 2.52584e+07 values per second.

If I turn off some of the error handling (adding -fno-trapping-math -fno-math-errno) I get

• Tiny: 3.11431e+08 values per second.
• Linear: 1.05646e+08 values per second.
• Garbage: 2.71923e+07 values per second.

which did not really change performance that much.

So it is now confirmed that the speed is data dependent. Approximately 10, 30 and 100 cycles are needed per value depending on the input data.

Using SIMD to calculate sin(double)

Agner Fog has written a SIMD library called vectorclass which provides the possibility to calculate sin.

This is not bit accurate as the GNU implementation. It uses Taylor series with highest term x^13 for sin. It does range reduction but no table lookup. For double and avx2 hardware, it calculates the results for four values at a time. It is very readable compared to the GNU implementation.

Using the same benchmark as above, the performance is:

• Tiny: 8
• Linear: 8
• Garbage: 25

cycles per element. It surprises me that it is data dependent.

Using SIMD to calculate sin(float)

Same as above, but with floats.

• Tiny: 2
• Linear: 2
• Garbage: 40

This is incredibly fast. The data dependency is even higher than for double.

Observations

• sin and cos are both calculated, regardless if both are needed. This warrants having a sincos function (see my proposal P0081R0 to the C++ committe about this).
• could (sacrificing accuracy) the polynomial be evaluated in another order to get less data dependendencies? See Estrin’s scheme
• Taylor expansion around 0 is nice because only the odd terms are needed. But could another polynomial be used instead, minimizing absolute tolerance? Something like a Chebyshev expansion.
• Could one instead of splitting the circle in four parts, split it in 2^N parts which in N steps could be rotated? That way, the range for which the Taylor expansion needs to be correct shrinks, and the necessary number of terms for a given accuracy is reduced. Seems like this does not pay off, because the error shrinks faster with increasing the number of terms than with shrinking the maximum input.

Error characteristics for polynomial approximations

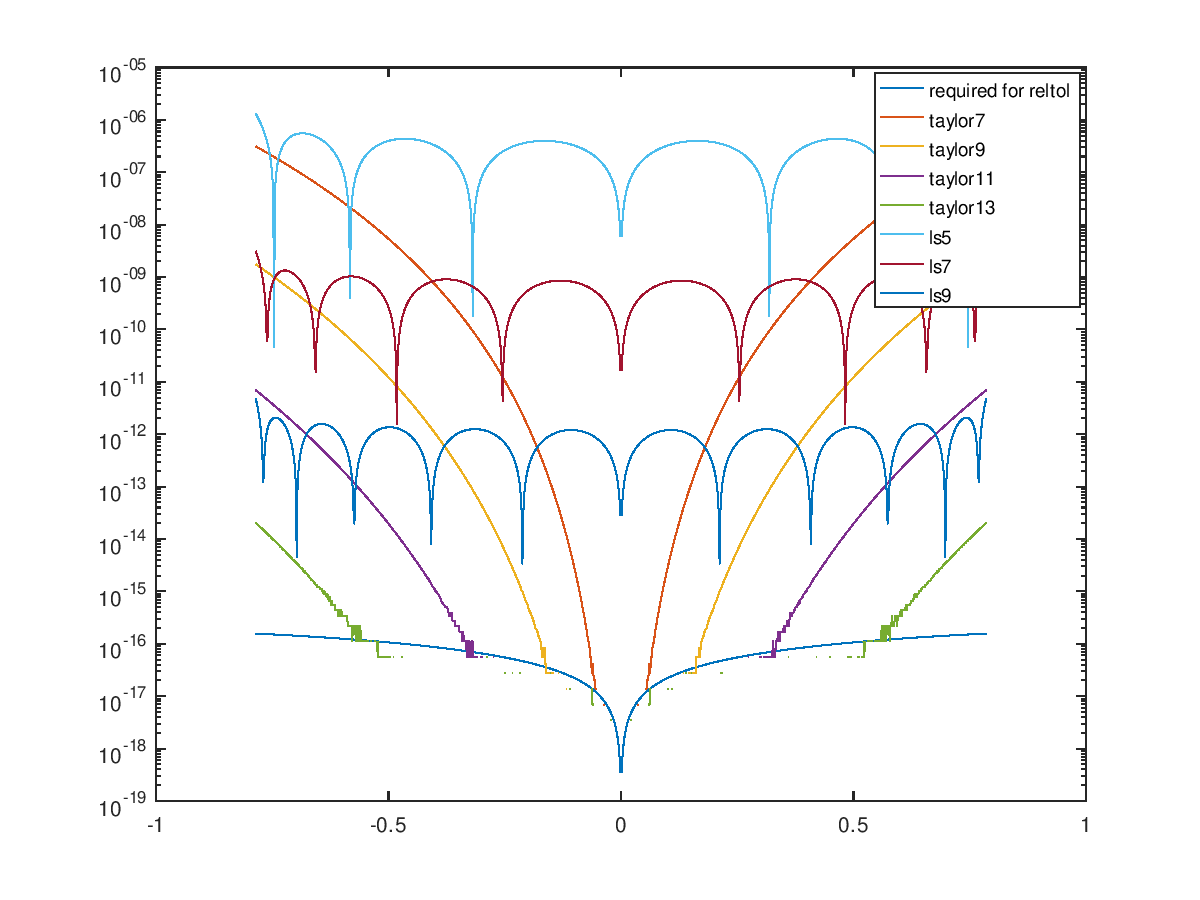
I studied the absolute error of different polynomial approximations over the interval |x|<pi/4. The required absolute tolerance to get the last bit correct is approximately |sin(x)|*2e-16, which is drawn as the line at the bottom in the figure.

I also added least squares approximation over the entire interval(with even coefficients forced to zero), which distribute the absolute error more evenly. One can see that the Taylor expansion is superior for small values of x, but at some point the least square curve is better.

If a limited absolute error is acceptable, the least squares approximation is better than Taylor. A nice property of the least square solution is that (because it is forced to be odd) is zero for x=0.

This got me thinking of switching between Taylor and least squares, depending on the octant. Calculating the octant is cheap, because it can be made as part of calculating the quadrant. Is it a variant of this the correction term lookup is using in GNU sincos?