Optimal production in Simcity builder

I started playing the Simcity (the Android version). It’s fun!

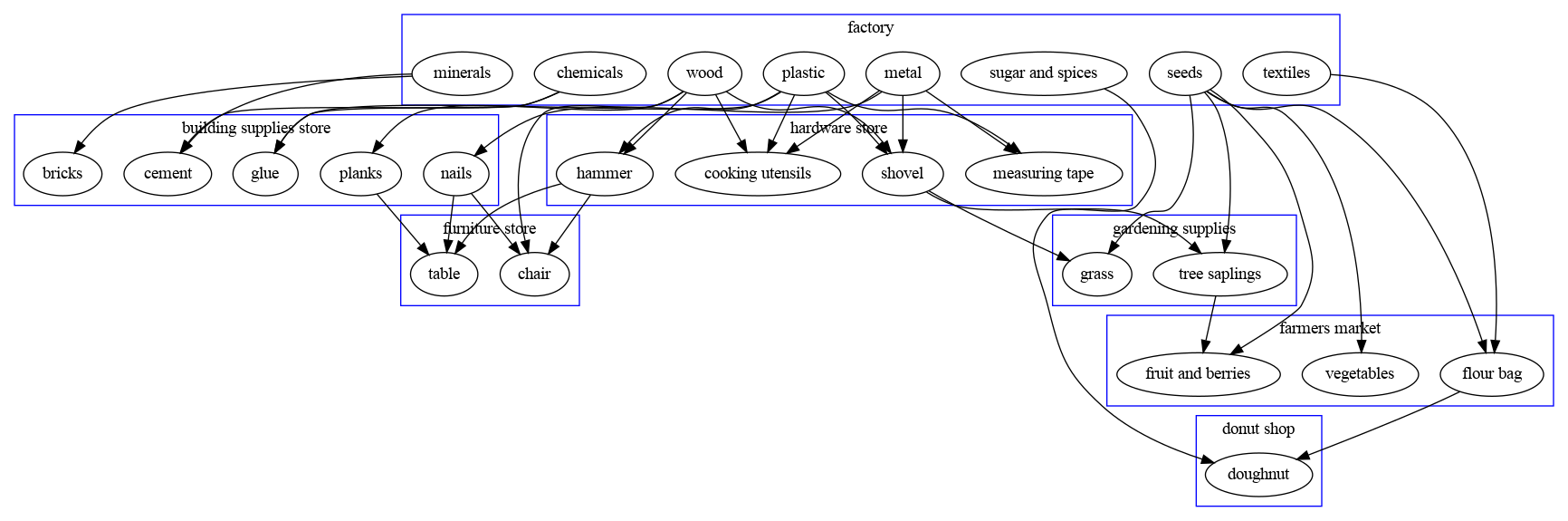
One can manufacture various materials and combine them to more refined products, which are possible to sell on something called the “trade depot”. For instance, one can make metal, then turn that metal into nails, combine it with wood to make a hammer. That hammer can be used to make a chair, which can be sold.

The production capacity is limited, and different materials take various amount of time to finish.

After a while, I started think which combination of materials and production which would maximize the profit. It turns out that this can be formulated as a linear programming problem. The difficulty is how to find the coefficients and formulation of the problem.

I started with writing a list of which materials/items exist, how long time they take to make, which materials they are constructed from and the market value. I am at level 19 and do not have all possible factories/shops. My basic factory has total 22 parallel slots. Some of the materials are difficult to sell, so I set their value to 0.

The most expensive item I can manufacture is a doughnut, which brings in 950 coins each.

The optimization is as follows:

Decide how many items to produce of each kind per hour, such that

• no factory operates at higher capacity than possible
• the production is not negative
• items needed to produce another item are accounted for
• no items are built up
• the total selling price of the net produced items is maximized

Introduce a vector x which is the produced items per hour.

Introduce the dependency matrix D (it is the adjacency matrix) such that to produce x, D‘x are consumed. The net production is x-D‘x per hour.

Introduce a vector p which contains the price per item, same size as x.

Let the matrix P be a matrix such that each row corresponds to a production unit (basic factories are lumped into one) and the columns refer to the different kinds of items. Put ones on the columns which that particular production unit can manufacture and zeros elsewhere.

Calculate the production time per item and put it in a vector f, the same size as x.

We can now for a given production x express how much factory time is needed as P×diag(f)×x. This can not exceed 1 (except for the basic factory, which has 22 parallel slots, so it may not exceed 22). Call this vector k.

The problem is now:

Maximize p‘×(x-D‘x)

with constraints:

• x>=0 (element wise)
• x-D‘x>=0 (element wise)
• P×diag(f)×x <= k (element wise)

I formulated this in octave using the glpk function. You can get the source file here.

The solution is: